Cálculo da Poligonal Fechada Topográfica: Guia Técnico Completo com Fórmulas, Etapas e Exemplos Práticos
Aprenda como calcular uma poligonal fechada na topografia com explicações claras, fórmulas e exemplos práticos.
Caderneta de Campo – Dados do Levantamento
O levantamento topográfico foi iniciado a partir da estação OPP, com coordenadas conhecidas e azimute base definido. Foram adotadas tolerâncias lineares e angulares compatíveis com levantamentos de precisão em poligonais fechadas. A seguir, apresentam-se os dados iniciais e os registros coletados em campo.
Dados Iniciais
- Azimute da direção OPP-1: 106º 52’ 07’’
- Coordenadas da estação OPP:
- X = 224,19 m
- Y = 589,25 m
- Tolerâncias:
- Angular: 10'' × m (m = número de ângulos medidos)
- Linear: 1:2000
Caderneta de Campo
| Ponto | Direção | Ângulo Horizontal | Distância (m) |
|---|---|---|---|
| OPP | OPP-1 | — | 100,18 |
| 1 | 1-2 | 246º 47’ 25’’ | 115,80 |
| 2 | 2-3 | 261º 29’ 34’’ | 116,68 |
| 3 | 3-4 | 301º 45’ 11’’ | 91,65 |
| 4 | 4-OPP | 148º 28’ 31’’ | 89,06 |
| 5 ≡ OPP | — | 301º 29’ 03’’ | — |
Croqui do Levantamento Topográfico
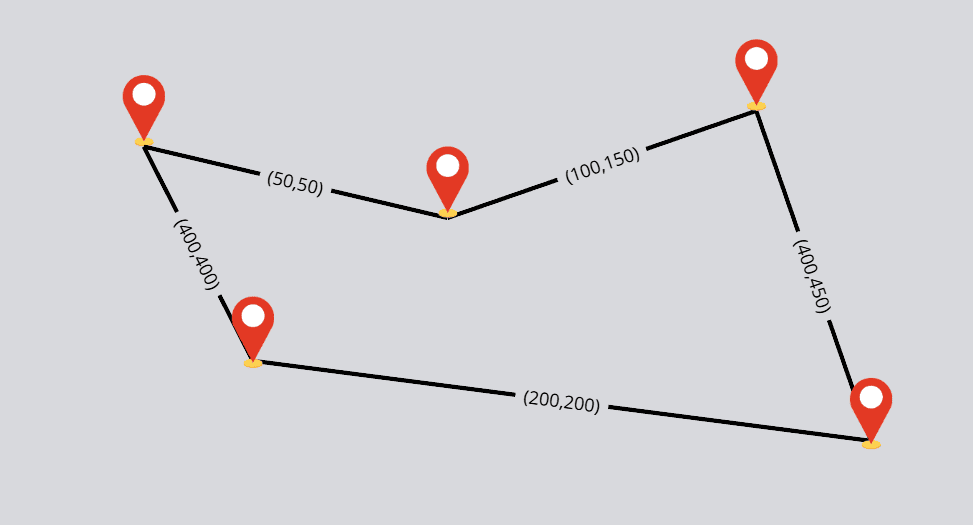
Figura 1 – Representação gráfica da poligonal fechada com orientação e pontos georreferenciados.
1) Verificação do Erro Angular
Fórmula:
ea = ΣÂ - (n + 2) × 180º- n = 5 (cinco vértices na poligonal)
- ΣÂ = 1259º 59’ 44’’
- Valor Teórico: (5 + 2) × 180º = 1260º
- Erro Angular (ea): 1259º 59’ 44’’ – 1260º = –16’’
Cálculo da Tolerância Angular:
εa = 10″ × m = 10″ × 5 = ±22″Como |ea| = 16″ e εa = ±22″, então: Dentro da Tolerância ✔️